数据结构&算法之美

基础

Remember: 所有数据的存取只有两种方式：线性和非线性。也就是数组和链表。所以不可能有其他数据结构的。高级的数据结构都是这二者的算法组合。

散列表HashTable

就是 JS 的 Map! 或是 Java 的 HashMap!

实质

将key值通过散列函数映射进对应的数组 index，存入数组中。

重难点

• 装载因子
  $散列表里的数据个数 \over 散列表长度$
• 散列冲突
  通过散列函数到数组 index 的映射处理结果可能碰撞，尤其是数组长度越小，碰撞可能性越大。
• 数组存储 > 开发寻址法: 数据较小
  对应实际情况，插入时，找到计算过后的数组对应位置。若该位已被占有，则会往后顺序查看，将数据放到第一顺位空位中。
  取值时，找到数组对应位置，若读出来 key 不是当前取值 key，则会往后继续寻找，若遇到第一个空位（p.s. 数据被删除后留下的空位会有特殊标记 不算）还没有找到，则说明当前数组没有此 key。
• 链表存储 > 链表法: 数据较多
  数组的每一位/槽 (slot) 里以链表的形式存储所有值。
  在链表到达一定长度时，可升级为红黑树~
• 动态扩容
  有个小优化的点。可以不一次性搬移数据到新数组，而是将阈值设为多个，慢慢的搬数据。因此在某个时间段上可能维护两个数组。

复杂度

所以严格意义上并不是O(1)，按存储方式，均需要加上散列冲突带来的多次寻址消耗。

实际应用

LRU缓存淘汰算法 / LinkedHashMap

两者都在 hashmap 的基础上搭配了链表:

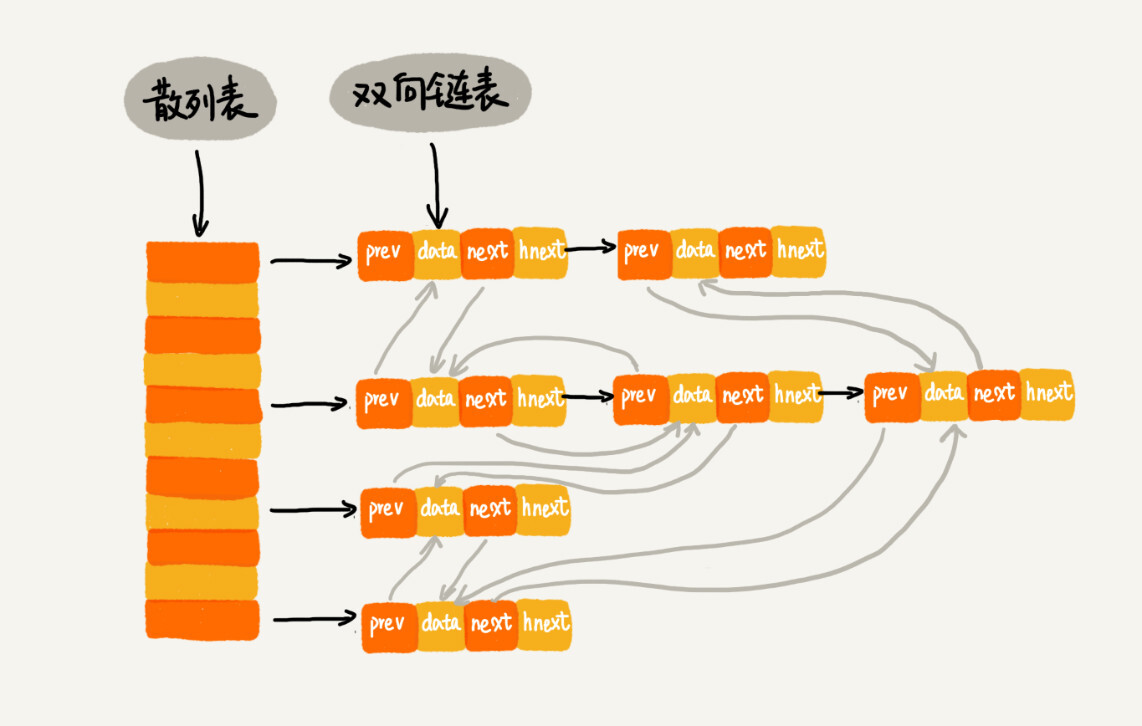
其实可以想成是对于链表的扩充。正因为链表不好以 O(1) 查找元素，所以才想办法通过固定来算法来决定链表元素的存储位置，实现以数组的方式来定位链表。当然反向来说，双向链表能以 O(1) 增删改元素，这也是对 hashmap 的反向加强。

Redis 有序集合

一个数据可能由多种数据结构同时维护，比如 redis 的跳表和 hashmap。前者适合以值区间查找，后者适合以键精确查找。

哈希算法

原则

将任意长度的二进制值串映射为固定长度的二进制值串，这个映射的规则就是哈希算法，而通过原始数据映射之后得到的二进制值串就是哈希值。 根据鸽巢理论，即无限的东西不能放进有限的坑里，所以一定会有碰撞。

用处

• 加密 //md5摘要
• 唯一标志 比如搜图片，不能拿图片名，拿图片二进制又比较耗时。所以我们可以给每一个图片取一个唯一标识，或者说信息摘要。可以从图片的二进制码串开头取 100 个字节，从中间取 100 个字节，从最后再取 100 个字节，然后将这 300 个字节放到一块，通过哈希算法得到一个哈希字符串，用它作为图片的唯一标识。
• 数据校验
• 散列函数
• 分布式系统：比如负载均衡、数据分片、分布式存储 关键在于需要将内容存储在不同的机器上，那么为了保持内容在机器上的存储一致性，需要确定哪块内容需要放到哪个机器上。通常会将内容哈希后对机器个数取模，结果即是。这样每次查找时都可以明确知道要去哪个机器上查找了，避免遍历所有机器。 但有个缺陷是所谓「雪崩效应」，即如果扩/缩容后，内容的存储机器可能会发生很大的不一致。为了避免每块内容的存储位置都发生变化，需要「一致性哈希算法」，真实做法是想成一个圆环，数据存储于顺时针遇到的第一个机器上。同时为了避免机器在圆环上分布偏向一角，可启用虚拟节点，即子节点的n个copy。ref

（二叉）树

基础

术语

(节点的)高度、深度、层数(从1开始)

分类

• 满二叉树
• 完全二叉树。除了最后一层的右侧可以有空位，其余位置都不行。 因为按数组存的时候不会有空位。p.s. 对于完全二叉树来说，下标从 2n+1 到 n 的都是叶子节点。

存储

• 链式
• 数组

遍历

• 前序、中序、后序 其中中序遍历可以实现以 O(n) 的形式输出有序数据序列
• 层级

二叉查找树

定义：左侧 < 中侧 < 右侧，若有重复数据，可以选择节点链表式存储，亦可以当做比当前节点小于等于的方式往右节点存。

操作

• 查找、新增都简单
• 删除:
• 如果目标节点是叶子节点直接删；
• 如果目标节点下只有一个节点，直接更新父节点的指针指向子节点；
• 如果目标节点下有两个节点，找到右侧节点链里最小的节点A，替换到目标节点。A必定没有左子节点，所以再按上述规则删除A；
• 时间复杂度 即 O(height)。最坏情况(只有单边链)下退化成链表 O(N)，最好情况(完全二叉树)下是 O($log_2n$)，看图即知和二分法查找很类似。

v.s. O(N)的散列表

• 排序方便：中序遍历 O(N) 即可有序输出；散列表排序难
• 散列表更复杂，比如扩缩容散列冲突

红黑树

近似于平衡二叉树(树的高度约为 $log_2n$)，避免普通二叉树在频繁更新下，复杂度退化的现象。

定义

• 根节点是黑色节点、叶子节点为空且也是黑色节点
• 每条路的黑色节点数一致
• 一条路上的红色节点需被黑色节点隔开

如何去思考？如果把红色节点都移除掉就相当于四叉树，高度肯定 < $log_2n$，那红色节点的高度没有黑色高，所以加起来也肯定 < $2log_2n$ 即符合要求。

实现

分为插入和删除，前者相对简略一些。和魔方公式很像，case by case来，就不背啦！

使用二叉树直观化复杂度

如果每层的计算复杂度一致，则是 每层复杂度*height；如果每层不一致，则每层复杂度+ ... +每层复杂度(一共height个)。 举个快排的例子，如果每次数据分为 $1/ 9$和$8/9$时，最短的一边是每次都$1/ 9$的那边，一共 $nlog_9n$；最长的那边则是 $nlog_{9/8}n$。

堆

每个节点都比子节点大/小的完全二叉树

操作

• 插入：插入到最后，从下到上堆化 复杂度logn
• 删除：将最后一个元素移至该位，从上到下堆化 复杂度logn

基于堆的排序

可以先将数组原地堆化…再排序 疯狂交换。整个复杂度也是$nlogn$。

实践

在我心中，这些实践=方案+存储方式。方案是最重要的，存储方式上堆可以被数组替代，只是效率要从 logn 降到 n。（总之…我不是很喜欢堆…可能暂时还不理解真实使用场景。）

比如合并有序小文件，动态求Top k数据，动态求中位数、90百分位数等。原理都是一样的。利用两个堆，一个大顶堆，一个小顶堆，随着数据的动态添加，动态调整两个堆中的数据，最后大顶堆的堆顶元素就是要求的数据。

图

术语

入度、出度、有向图、无向图、带权图

存储方式

• 二维数组：邻接矩阵（Adjacency Matrix）两个有联系的点分别作为数组的index值。比较直接，但耗空间。
• 散列表：邻接表 每个index项都会以链表/二叉树的形式存储与这个点有关的其他点

实践

好友关系、交通图、思维导图