part1-week3
Insertion sort
public class Insertion {
public static void sort(Comparable[] a) {
int N = a.length;
for (int = 0; i< N; i++) {
for (int j = i; j > 0 && less(a[j], a[j-1]); j--) {
exch(a, j, j-1);
}
}
}
}
Selection sort
public class Selection {
public static void sort(Comparable[] a) {
int N = a.length;
for (in i = 0; i < N; i++) {
int min = i;
for (int j = i+1; j < N; j++) {
if(less(a[j], a[min])) {
min = j;
}
}
exch(a, i, min); // long-distance exchange might move an item past some equal item.
}
}
}
Shellsort
public class Shell {
public static void sort(Comparable[] a) {
int N = a.length;
int h = 1;
while (h < N/3) h = 3*h + 1;
while (h >= 1) {
for (int i = h; i < N; i++) {
for (int j = i; j > h && less(a[j], a[j-h]); j -= h) {
exch(a, j, j-h);
}
}
h = h/3;
}
}
}
MergeSort
auxiliary array: 备用数组 (to hold the data)
(maintain) indices: 索引 - the current entry in the reslut
Increment that pointer j.
quite straightforward in the demo.
a[], aux[]
Overview: Divide array into two halves. Recursively sort each half. Merge two halves.
public class Merge {
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
assert isSorted(a, lo, mid);
assert isSorted(a, mid+1, hi); // precondition
for(int k = lo; k <= hi; k++)
aux[k] = a[k];
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
assert isSorted(a, lo, hi);
}
private static void sort(Comparable[] a,){
}
}
Notes:
-
divide and conquer
-
not create aux in recursive // create arrays is costly
Complexity:
- NlogN compares, 6NlgN array access.


- Memory: (proportional to) N
Improvement:
- use insertion sort for small subarrays
- when the biggest element in one half is smaller than the smallest element in the other half, the order is done, no need for further recursive merge. This would decrease the complexity for sorting an sorted array to linearity.
- Instead of copying over to an auxiliary array, you can switch the role of input and the auxiliary array everytime you make a recursive call.
More:
- inplace merge (much more complex)
Qs:
- How many compares does mergesort—the pure version without any optimizations—make to sort an input array that is already sorted?
A. Constant B. logarithmic C. linear D. linearthmic
It makes ~ 1/2N log2 N compares, which is the best case for mergesort. We note that the optimized version that checks whether a[mid] \le a[mid+1]a[mid]≤a[mid+1] requires only n - 1n−1 compares.
[出题:查看动画 visualization,选择是哪种 merge 形式]
Sorting Complexity
- Cost model: Operation counts ~ #the number compares
- (某个问题的)Upper bound: ..by some algorithm ~ NlgN from mergesort (Some algorithm can do this 一般指目前最好的算法)
- (某个问题的)Lower bound: ..all algorthms (任意算法的复杂度都在 lower bound 之上, No algorithm can do better. 所以只要知道这个数值,就可以一眼看出来算法的可优化上限了,我觉得很有道理哇!) 但是前提是数据没有 partially-ordered, 也没有 dupilcate keys 之类的
- (某个问题的)Optimal algorithm(whose Upper bound == Lower bound, so has the best possible cost guarantee)
对于找解决某一问题的那一类算法的lower bound,我们通常有两种办法,
1)decision tree 我们通过分析决策树的方法来得到 lower bound(这也是算法导论里面提到的方法)
2)adversary strategy 这个确实不好翻译,竞争者策略?! 当然这个方法要比上面的decision tree得到的lower bound更tight一些。(当然这个也不绝对,还要看你的strategy) ######
- Big O: O(g(n)) = {f(n) : 存在一个正常数c,和一个 N0, 对于所有的N>N0, 0<= f(n) <= c*g(n)} 所以相当于 f(n) 的一个 upper bound
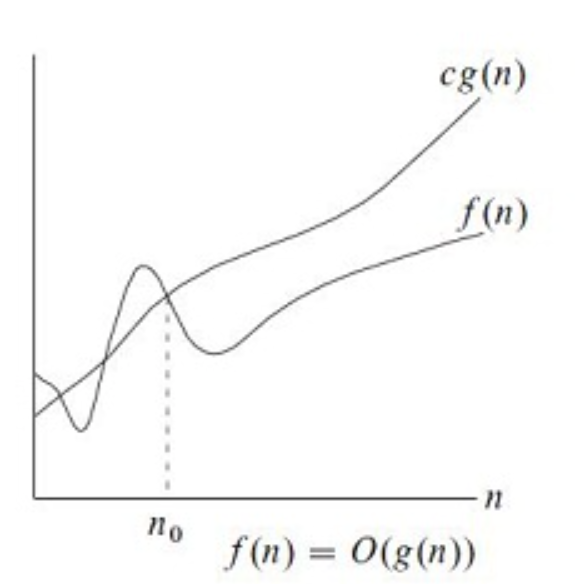
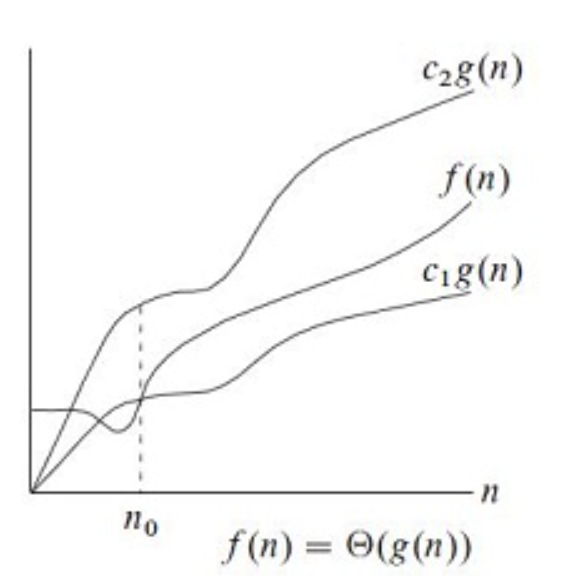
- Omega: Omega(g(n)) = {f(n): 存在一个正常数c,和一个 N0, 对于所有的N>N0, 0<= c*g(n) <= f(n) } 所以相当于 f(n) 的一个 lower bound
Decision Tree


Preopsition: Any compare-based sorting algorithm must use at least lg(N!)~NlgN compares in the worst case.
Pf.
- Assume array consists of N distinct values a~1~ through a~N~.
- Worst case dictated by height h of decision tree.
- Binary tree of height h has at most 2^h^ leaves.(complete tree)
- N! Different orderings => at least N! leaves.
- 2^h^ >= #leaves >=N!
- h >= lgN! ~ (is proportional to) NlgN (by Stirling's formula)
- Lower bound ~ NlgN
- Mergesort is optimal with respect to #compares
- So, dont try to desgin sorting algorithm that guarantees 1/2NlgN compares.
Stability
Q: Which sorts are stable?
A: Insertion sort and merge sort (but no selection sort or shell sort). Always use less than vs less than or equal to.
QuickSort

// https://github.com/ShafayetB/Coursera/tree/master/Algorithms-Part%20I/Assignments